（本小题满分12分）随机抽取某中学高三年级甲乙两班各10名同学，测量出他们的身高（单位：cm），获得身高数据的茎叶图如图，其中甲班有一个数据被污损．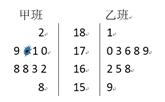
（Ⅰ）若已知甲班同学身高平均数为170cm，求污损处的数据；
（Ⅱ）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高176cm的同学被抽中的概率．
中，
，
是
上的一个动点，
最小时，求
的值。
时，求
中,
,
分别是角
所对的边.
； (Ⅱ)若
,
,求
，
。
；（2）求
的最大值及相应的
值；
中，已知
，
，
．
的值；（Ⅱ）求
的值相关知识点
推荐套卷
（本小题满分12分）随机抽取某中学高三年级甲乙两班各10名同学，测量出他们的身高（单位：cm），获得身高数据的茎叶图如图，其中甲班有一个数据被污损．
（Ⅰ）若已知甲班同学身高平均数为170cm，求污损处的数据；
（Ⅱ）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高176cm的同学被抽中的概率．
粤公网安备 44130202000953号