某港口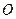 要将一件重要物品用小艇送到一艘正在航行的轮船上.在
要将一件重要物品用小艇送到一艘正在航行的轮船上.在 小艇出
小艇出 发时,轮船位于港口
发时,轮船位于港口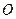 北偏西
北偏西 且与该港口相距20海里的
且与该港口相距20海里的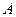 处,并以30海
处,并以30海 里/小时的航行速度沿正东方向匀速行驶.假设该小船沿直线方向以
里/小时的航行速度沿正东方向匀速行驶.假设该小船沿直线方向以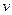 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过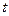 小时与轮船相遇.
小时与轮船相遇.
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
相关知识点
推荐套卷
 届亚运会于
届亚运会于 年
年 月
月 日至
日至 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱. 列联表:
列联表: 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关? 人会外语),抽取
人会外语),抽取 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中
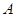 、
、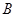 、
、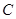 为
为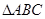 的三个内角,且其对边分别为
的三个内角,且其对边分别为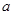 、
、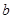 、
、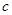 ,若
,若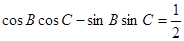 .
. ,求
,求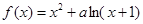 有两个极值点
有两个极值点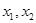 ,且
,且 .
.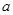 的取值范围;
的取值范围;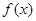 的单调性;
的单调性;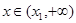 ,都有
,都有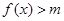 成立,求实数
成立,求实数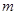 的取值范围.
的取值范围.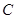 :
:
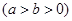 的离心率为
的离心率为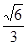 ,过右焦点
,过右焦点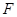 且斜率为
且斜率为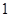 的直线交椭圆
的直线交椭圆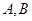 两点,
两点,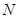 为弦
为弦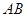 的中点,
的中点,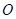 为坐标原点.
为坐标原点. 的斜率
的斜率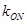 ;
;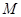 ,都存在
,都存在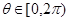 ,使得
,使得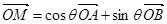 成立.
成立.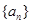 中,
中,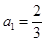 ,且对任意的
,且对任意的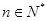 都有
都有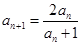 .
.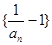 是等比数列;
是等比数列;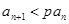 ,求实数
,求实数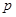 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号