(本题12分)如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,m),A(n,m),且(m–4)2+n2–8n=–16,过C点作∠ECF分别交线段AB、OB于E、F两点.
(1)求A点的坐标.
(2)若OF+BE=AB,求证:CF=CE.
(3)如图(2),若∠ECF=45°,给出两个结论:OF+AE–EF的值不变;OF+AE+EF的值不变.其中有且只有一个结论正确,请你判断出正确的结论,并加以证明和求出其值.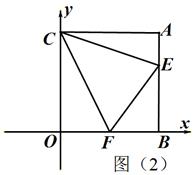
相关知识点
推荐套卷
 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支. (单位:km),行驶过程中平均耗油量为
(单位:km),行驶过程中平均耗油量为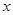 (单位:升/km).
(单位:升/km). 的取值范围;
的取值范围; ,该车返回出发地是否需要加油?若需要,试求出至少需加多少油,若不需要,请说明理由。
,该车返回出发地是否需要加油?若需要,试求出至少需加多少油,若不需要,请说明理由。 粤公网安备 44130202000953号
粤公网安备 44130202000953号