(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为 ;
②线段AD,BE之间的数量关系为 ;
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;
(3)如图3,在正方形ABCD中,CD= ,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.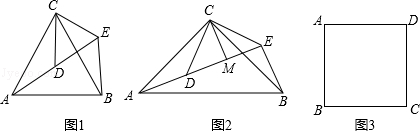
推荐套卷
 .
. .
. ,其中
,其中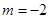 .
.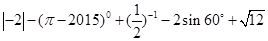 .
.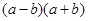 = ;
= ;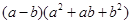 = ;
= ;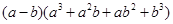 = .
= . = (其中n为正整数,且
= (其中n为正整数,且 ).
). .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号