在元旦联欢会上，有一个开盒有奖的游戏，两只外观一样的盒子，一只装有奖品，一只
是空的，游戏规定：每人每次游戏时主持人先混合盒子再拿出来，参加游戏的同学随机打开其中一只，若
有奖品，就获得该奖品，若是空盒子，就表演一个节目．
（1）两个人参加游戏，都获奖的概率为_______．
（2）n个人参加游戏，全部获奖的概率为________．
（3）现取三只外观一样的盒子，一只内有奖品，另两只空盒子，游戏规则不变．两个人参加游戏，用画树形
图法求至少有一个人表演节目的概率．
相关试题
.
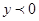时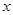
的取值范围.
的正弦、余弦值.
（本小题满分8分）
已知抛物线y＝ax2＋bx＋6与x轴交于A、B两点（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，且OB=
OC，tan∠ACO=
，顶点为D．（1）求点A的坐标．
（2）求直线CD与x轴的交点E的坐标.
（3）在此抛物线上是否存在一点F，使得以点A、C、E、F为顶点的四边形是平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．
（4）若点M（2，y）是此抛物线上一点，点N是直线AM上方的抛物线上一动点，当点N运动到什么位置时，四边形ABMN的面积S最大? 请求出此时S的最大值和点N的坐标．
（5）点P为此抛物线对称轴上一动点，若以点P为圆心的圆与（4）中的直线AM及x轴同时相切，则此时点P的坐标为.
（本小题满分8分）
已知，在△ABC中，∠BAC=90°，AB=AC，BC=
，点D、E在BC边上（均不与点B、C重合，点D始终在点E左侧），且∠DAE＝45°．（1）请在图①中找出两对相似但不全等的三角形，写在横线上，；
（2）设BE＝m，CD＝n，求m与n的函数关系式，并写出自
变量n的取值范围；（3）如图②，当BE＝CD时，求DE的长；
（4）求证：无论BE与CD是否相等，都有DE2=BD2+CE2.
，tan∠ADC=2．
相关知识点
推荐套卷
粤公网安备 44130202000953号