(本小题满分8分)
已知,在△ABC中,∠BAC=90°,AB=AC,BC= ,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.(1)请在图①中找出两对相似但不全等的三角形,写在横线上 , ;
(2)设BE=m,CD=n,求m与n的函数关系式,并写出自
 变量n的取值范围;
变量n的取值范围;(3)如图②,当BE=CD时,求DE的长;
(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.

相关知识点
推荐套卷
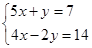
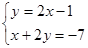
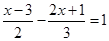
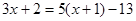
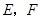 分别为边
分别为边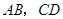 的中点,连接
的中点,连接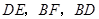 .
.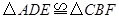 .
.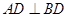 ,则四边形
,则四边形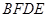 是什么特殊四边形?请证明你的结论.
是什么特殊四边形?请证明你的结论.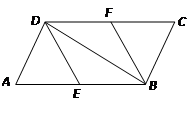
 粤公网安备 44130202000953号
粤公网安备 44130202000953号