探究:当a=5,b=8时,① =9, ②
=9, ②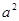 -2ab+
-2ab+ =9.
=9.
当a=2,b=-3时,① = ,②
= ,②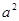 -2ab+
-2ab+ = .
= .
(每空1分,共2分)
猜想:这两个代数式之间的关系是: (用含a、b的等式表示).
应用:利用你的发现,求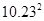 -2×10.23×9.23+
-2×10.23×9.23+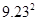 的值.
的值.
相关知识点
推荐套卷
探究:当a=5,b=8时,① =9, ②
=9, ②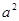 -2ab+
-2ab+ =9.
=9.
当a=2,b=-3时,① = ,②
= ,②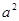 -2ab+
-2ab+ = .
= .
(每空1分,共2分)
猜想:这两个代数式之间的关系是: (用含a、b的等式表示).
应用:利用你的发现,求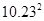 -2×10.23×9.23+
-2×10.23×9.23+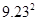 的值.
的值.