(本小题满分14分)已知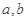 是实数,函数
是实数,函数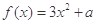 ,
,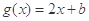 ,若
,若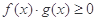 在区间
在区间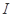 上恒成立,则称
上恒成立,则称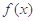 和
和 在区间
在区间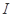 上为“
上为“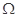 函数”.
函数”.
(1)设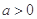 ,若
,若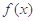 和
和 在区间
在区间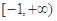 上为“
上为“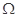 函数”,求实数
函数”,求实数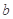 的取值范围;
的取值范围;
(2)设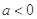 且
且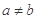 ,若
,若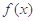 和
和 在以
在以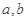 为端点的开区间上为“
为端点的开区间上为“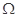 函数”,求
函数”,求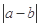 的最大值.
的最大值.
推荐套卷
(本小题满分14分)已知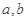 是实数,函数
是实数,函数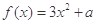 ,
,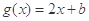 ,若
,若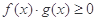 在区间
在区间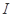 上恒成立,则称
上恒成立,则称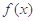 和
和 在区间
在区间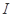 上为“
上为“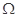 函数”.
函数”.
(1)设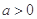 ,若
,若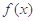 和
和 在区间
在区间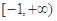 上为“
上为“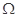 函数”,求实数
函数”,求实数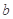 的取值范围;
的取值范围;
(2)设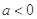 且
且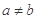 ,若
,若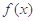 和
和 在以
在以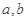 为端点的开区间上为“
为端点的开区间上为“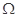 函数”,求
函数”,求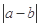 的最大值.
的最大值.