两个相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.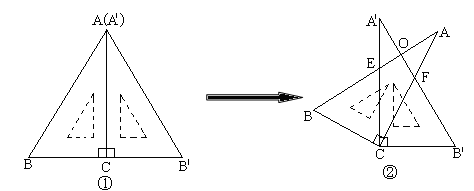
(1)求证:△BCE≌△B′CF。
(2)当旋转角等于30°时,AB与A′B′垂直吗?请说明理由。
推荐套卷
两个相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.
(1)求证:△BCE≌△B′CF。
(2)当旋转角等于30°时,AB与A′B′垂直吗?请说明理由。