（本小题满分14分）直棱柱
中，底面ABCD是直角梯形，∠BAD＝∠ADC＝90°，
．
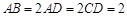（1）求证：AC⊥平面BB1C1C；
（2）在A1B1上是否存一点P，使得DP与平面BCB1与平面ACB1都平行？证明你的结论．
的所有实数
，求使不等式
恒成立的
取值范围.
、
∈R且
，求
的范围.
}中，
="13" ，且前
项的算术平均数等于第
若
，求实数a的取值范围．
且
，求
的最大值．相关知识点
推荐套卷
（本小题满分14分）直棱柱中，底面ABCD是直角梯形，∠BAD＝∠ADC＝90°，．
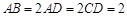（1）求证：AC⊥平面BB1C1C；
（2）在A1B1上是否存一点P，使得DP与平面BCB1与平面ACB1都平行？证明你的结论．
粤公网安备 44130202000953号