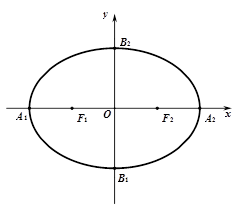
(本小题满分14分)如图所示,椭圆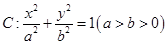 的左右焦点分别为
的左右焦点分别为 ,点
,点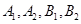 为椭圆
为椭圆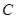 与坐标轴的交点,其中
与坐标轴的交点,其中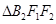 为等边三角形且面积为
为等边三角形且面积为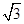 .
.
(1)求椭圆C的标准方程;
(2)过椭圆C的右顶点A2作两条互相垂直的直线分别和椭圆交于另一点P,Q,试判断直线PQ是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
推荐套卷
(本小题满分14分)如图所示,椭圆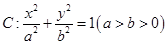 的左右焦点分别为
的左右焦点分别为 ,点
,点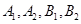 为椭圆
为椭圆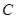 与坐标轴的交点,其中
与坐标轴的交点,其中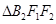 为等边三角形且面积为
为等边三角形且面积为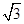 .
.
(1)求椭圆C的标准方程;
(2)过椭圆C的右顶点A2作两条互相垂直的直线分别和椭圆交于另一点P,Q,试判断直线PQ是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.