图1是一个正方体的表面展开图，MN和PB是两条面对角线，请在图2的正方体中将MN和PB画出来，并就这个正方体解决下列问题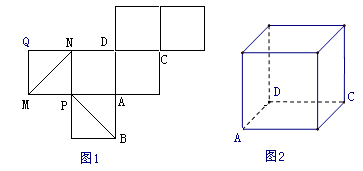
（1） 求证：MN//平面PBD； （2）求证：AQ
平面PBD；
（3）求二面角P-DB-M的余弦值。
相关试题
．
的最小正周期；
上的最小值，并写出
值．
,
.
；
介于
与
之间，且距
之间的距离是否可能为整数？若有，则求出这个整数；若没有，已知半径为2，圆心在直线
上的圆C.
（Ⅰ）当圆C经过点A（2,2）且与
轴相切时，求圆C的方程；
（Ⅱ）已知E(1，1),F(1，-3),若圆C上存在点Q，使
,求圆心的横坐标
的取值范围.
.
，求
的最小值；
的图象，使得
的图象有公共点且在公共点处切线相同.
中，
，
，
，D为BC中点.
;
;
的正弦值.推荐套卷
图1是一个正方体的表面展开图，MN和PB是两条面对角线，请在图2的正方体中将MN和PB画出来，并就这个正方体解决下列问题
（1） 求证：MN//平面PBD； （2）求证：AQ平面PBD；
（3）求二面角P-DB-M的余弦值。
已知半径为2，圆心在直线上的圆C.
（Ⅰ）当圆C经过点A（2,2）且与轴相切时，求圆C的方程；
（Ⅱ）已知E(1，1),F(1，-3),若圆C上存在点Q，使,求圆心的横坐标的取值范围.
粤公网安备 44130202000953号