如图,在数轴上点A、B、C表示的数分别为-2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
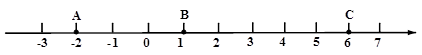
(1)则AB=,BC=,AC=;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动。请问:BC-AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
(3)由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:随着运动时间t的变化, AB、BC、AC之间是否存在类似于(1)的数量关系?请说明理由.