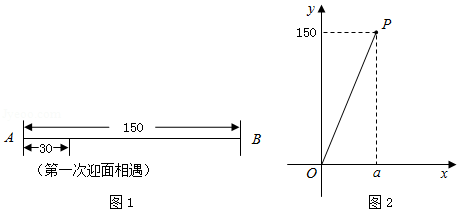
学校数学兴趣小组利用机器人开展数学活动.
在相距150个单位长度的直线跑道
上,机器人甲从端点
出发,匀速往返于端点
、
之间,机器人乙同时从端点
出发,以大于甲的速度匀速往返于端点
、
之间.他们到达端点后立即转身折返,用时忽略不计.
兴趣小组成员探究这两个机器人迎面相遇的情况,这里的”迎面相遇“包括面对面相遇、在端点处相遇这两种.
(观察)
①观察图1,若这两个机器人第一次迎面相遇时,相遇地点与点
之间的距离为30个单位长度,则他们第二次迎面相遇时,相遇地点与点
之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点
之间的距离为40个单位长度,则他们第二次迎面相遇时,相遇地点与点
之间的距离为 个单位长度;
(发现)
设这两个机器人第一次迎面相遇时,相遇地点与点
之间的距离为
个单位长度,他们第二次迎面相遇时,相遇地点与点
之间的距离为
个单位长度.兴趣小组成员发现了
与
的函数关系,并画出了部分函数图象(线段
,不包括点
,如图2所示).
①
;
②分别求出各部分图象对应的函数表达式,并在图2中补全函数图象;
(拓展)
设这两个机器人第一次迎面相遇时,相遇地点与点
之间的距离为
个单位长度,他们第三次迎面相遇时,相遇地点与点
之间的距离为
个单位长度.
若这两个机器人第三次迎面相遇时,相遇地点与点
之间的距离
不超过60个单位长度,则他们第一次迎面相遇时,相遇地点与点
之间的距离
的取值范围是 .(直接写出结果)