为了解某校七、八年级学生的睡眠情况,随机抽取了该校七、八年级学生部分学生进行调查.已知抽取七年级与八年级的学生人数相同,且八年级学生的D组有15人,利用抽样所得的数据绘制所示的统计图表.
睡眠情况分组表(单位:时)
组别
|
睡眠时间x
|
A
|
x≤7.5
|
B
|
7.5≤x≤8.5
|
C
|
8.5≤x≤9.5
|
D
|
9.5≤x≤10.5
|
E
|
x≥10.5
|
根据图表提供的信息,回答下列问题:
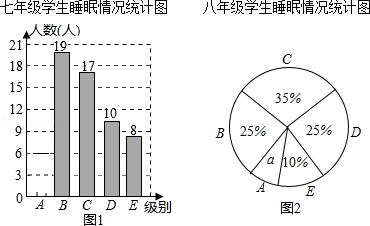
(1)此次调查抽取样本容量是 ;七年级学生睡眠时间在A组的有 人;并补全七年级学生睡眠情况统计图;
(2)求“八年级学生睡眠情况统计图”中的a及a对应的扇形的圆心角度数;
(3)抽取的样本中七、八年级学生睡眠时间在C组的共有多少人?
(4)已知该校七年级学生有800人,八年级学生有850人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生睡眠时间合格的共有多少人?