如图，已知双曲线
＝1（a>0，b>0），定点
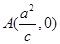（c是双曲线的半焦距），双曲线虚轴的下端点为B.过双曲线的右焦点F（c，0）作垂直于x轴的直线交双曲线于点P，若点D满足
（O为原点），且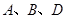
三点共线．
（1）求双曲线的离心率；
（2）若a＝2，过点B的直线l交双曲线的左、右支于M、N两点，且△OMN的面积S△OMN＝
，求l的方程．
，集合
．
，求
和
；
，求实数
的取值范围．
，求
的值
},集合B={（x,y）
,且0
}，又A
，求实数m的取值范围.
)上单调递增，并且f (x)<0对一切
成立，试判断
在(－
，且
，求证：
．相关知识点
推荐套卷
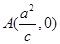如图，已知双曲线＝1（a>0，b>0），定点（c是双曲线的半焦距），双曲线虚轴的下端点为B.过双曲线的右焦点F（c，0）作垂直于x轴的直线交双曲线于点P，若点D满足 （O为原点），且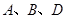三点共线．
（1）求双曲线的离心率；
（2）若a＝2，过点B的直线l交双曲线的左、右支于M、N两点，且△OMN的面积S△OMN＝，求l的方程．
粤公网安备 44130202000953号