如图,长为50cm,宽为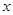 cm的大长方形被分割为8小块,除阴影A、B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为
cm的大长方形被分割为8小块,除阴影A、B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为 cm.
cm.
(1)从图可知,每个小长方形较长一边长是 cm(用含 的代数式表示);
的代数式表示);
(2)求图中两块阴影A、B的周长和(可以用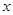 的代数式表示);
的代数式表示);
(3)分别用含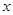 ,
, 的代数式表示阴影A、B的面积,并求
的代数式表示阴影A、B的面积,并求 为何值时两块阴影部分的面积相等.
为何值时两块阴影部分的面积相等.
相关知识点
推荐套卷
如图,长为50cm,宽为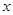 cm的大长方形被分割为8小块,除阴影A、B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为
cm的大长方形被分割为8小块,除阴影A、B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为 cm.
cm.
(1)从图可知,每个小长方形较长一边长是 cm(用含 的代数式表示);
的代数式表示);
(2)求图中两块阴影A、B的周长和(可以用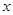 的代数式表示);
的代数式表示);
(3)分别用含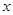 ,
, 的代数式表示阴影A、B的面积,并求
的代数式表示阴影A、B的面积,并求 为何值时两块阴影部分的面积相等.
为何值时两块阴影部分的面积相等.