(本小题满分12分)某医药研究所研发了一种新药,如果成年人按规定的计量服用,据监测:服药后每毫升血液中的含药量 (微克)与时间
(微克)与时间 (时)之间近似满足如图所示的曲线。
(时)之间近似满足如图所示的曲线。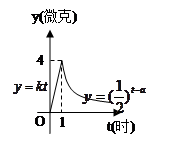
(1)写出服药后 与
与 之间的函数关系式
之间的函数关系式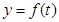 ;
;
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效。试求服药一次治疗疾病的有效时间。
推荐套卷
(本小题满分12分)某医药研究所研发了一种新药,如果成年人按规定的计量服用,据监测:服药后每毫升血液中的含药量 (微克)与时间
(微克)与时间 (时)之间近似满足如图所示的曲线。
(时)之间近似满足如图所示的曲线。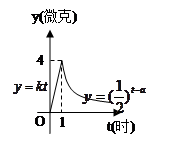
(1)写出服药后 与
与 之间的函数关系式
之间的函数关系式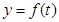 ;
;
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效。试求服药一次治疗疾病的有效时间。