（本小题满分12分）
如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA＝30°，PA＝AB＝2，点E为线段PB的中点，点M在AB上，且OM∥AC.
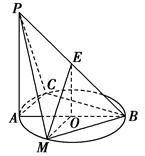
（1）求证：平面MOE∥平面PAC；
（2）求证：平面PAC⊥平面PCB；
（3）设二面角M－BP－C的大小为θ，求
的值．
相关试题
的前10项．试根据该程序给出的数列关系，
和第4项
；
；
：
，
：
，求当
为何值时，
.
时，讨论
的单调性；
当
时，若对任意
，存在
，使
，求实数
取值范围.
满足：
，
，
．
及
（n
N*），求数列
的前n项和
．
，其图象过点（
,
）．
的值；
的图象上各点的横坐标缩短到原来的
的图象，求函数
在[0, 
]上的最大值和最小值．推荐套卷
（本小题满分12分）如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA＝30°，PA＝AB＝2，点E为线段PB的中点，点M在AB上，且OM∥AC.
（1）求证：平面MOE∥平面PAC；
（2）求证：平面PAC⊥平面PCB；
（3）设二面角M－BP－C的大小为θ，求的值．
粤公网安备 44130202000953号