如图，是小亮晚上在广场散步的示意图，图中线段AB表示站立在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯的位置．
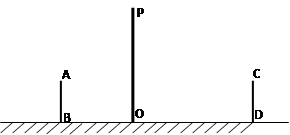
（1）在小亮由B处沿BO所在的方向行走到达O处的过程中，他在地面上的影子长度的变化情况为 ；
（2）请你在图中画出小亮站在AB处的影子；
（3）当小亮离开灯杆的距离OB=4.2m时，身高（AB）为1.6m的小亮的影长为1.6m，问当小亮离开灯杆的距离OD=6m时，小亮的影长是多少m？
相关试题
如图，是小亮晚上在广场散步的示意图，图中线段AB表示站立在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯的位置．
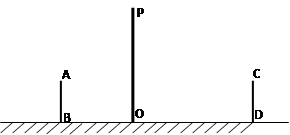
（1）在小亮由B处沿BO所在的方向行走到达O处的过程中，他在地面上的影子长度的变化情况为 ；
（2）请你在图中画出小亮站在AB处的影子；
（3）当小亮离开灯杆的距离OB=4.2m时，身高（AB）为1.6m的小亮的影长为1.6m，问当小亮离开灯杆的距离OD=6m时，小亮的影长是多少m？
，求代数式
的值.
中，
.
⊥
于点
，且
，
⊥
交
.求证：
.
.
（
），∠GEF的两边分别交矩形的边于点M，点N．当△MEN为等腰三角形时，求此时△MEN的面积．
粤公网安备 44130202000953号