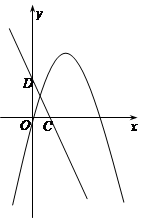如图，一次函数y=－2x+t的图象与x轴，y轴分别交于点C，D.
（1）求点C，点D的坐标；
（2）已知点P是二次函数y=－x2+3x图象在y轴右侧部分上的一个动点， 若以点C，点D为直角顶点的△PCD与△OCD相似。求t的值及对应的点P的坐标.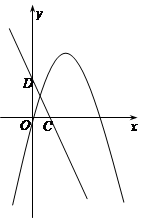
相关试题
的异侧有
、
两个村庄，现两村要合资建一条公路，要使费最少应按怎样的路线建造？请说明理由.
、
、
，利用尺规，作出一条线段，使它等于
相关知识点
推荐套卷
如图，一次函数y=－2x+t的图象与x轴，y轴分别交于点C，D.
（1）求点C，点D的坐标；
（2）已知点P是二次函数y=－x2+3x图象在y轴右侧部分上的一个动点， 若以点C，点D为直角顶点的△PCD与△OCD相似。求t的值及对应的点P的坐标.
粤公网安备 44130202000953号