如图1,四边形ABCD是边长为 的正方形,长方形AEFG的宽
的正方形,长方形AEFG的宽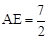 ,长
,长 .将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.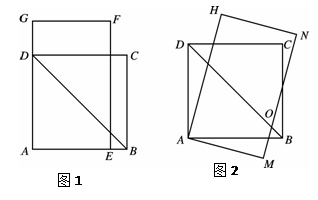
(1)求 的度数;
的度数;
(2)在图2中,求D、N两点间的距离;
(3)若把长方形AMNH绕点A再顺时针旋转15°得到长方形ARTZ,请问此时点B在矩形ARTZ的内部、外部、还是边上?并说明理由.
如图1,四边形ABCD是边长为 的正方形,长方形AEFG的宽
的正方形,长方形AEFG的宽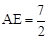 ,长
,长 .将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
(1)求 的度数;
的度数;
(2)在图2中,求D、N两点间的距离;
(3)若把长方形AMNH绕点A再顺时针旋转15°得到长方形ARTZ,请问此时点B在矩形ARTZ的内部、外部、还是边上?并说明理由.