已知:抛物线 与
与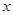 轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线
轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线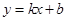 经过点A、C.
经过点A、C.(1)求点D的坐标和直线AC的解析式;
(2)点
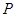 为抛物线上的一个动点,求使得
为抛物线上的一个动点,求使得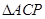 的面积与
的面积与 的面积相等的点
的面积相等的点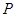 的坐标.
的坐标.
相关知识点
推荐套卷
已知:抛物线 与
与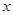 轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线
轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线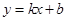 经过点A、C.
经过点A、C.(1)求点D的坐标和直线AC的解析式;
(2)点
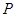 为抛物线上的一个动点,求使得
为抛物线上的一个动点,求使得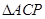 的面积与
的面积与 的面积相等的点
的面积相等的点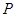 的坐标.
的坐标.