已知函数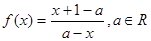
。利用函数
构造一个数列
，方法如下：对于定义域中给定的
，令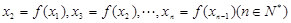
，…
如果取定义域中任一值作为，都可以用上述方法构造出一个无穷数列。
（1）求实数a的值；
（2）若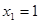
，求
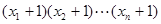的值；
（3）设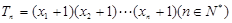
,试问：是否存在n使得
成立，若存在，试确定n及相应的的值;若不存在，请说明理由。
为⊙
中的弦，弧
为
，弧
且
，
，求半径
,
为直线
上的两点，且
=(
,
), 
(
)和
(
)在
分别为
,且
=
中，
，
，
与
交于点
设
,
在线段
上取一点
，线段
上取一点
，使
过点
设
，
，求证：
满足条件
时，求变量
的取值范围
，点
是双曲线的渐近线与椭圆的一个交点，求双曲线与椭圆的方程．推荐套卷
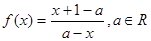已知函数。利用函数构造一个数列，方法如下：对于定义域中给定的，令，…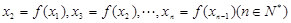
如果取定义域中任一值作为，都可以用上述方法构造出一个无穷数列。
（1）求实数a的值；
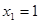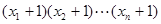（2）若，求的值；
（3）设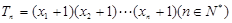,试问：是否存在n使得成立，若存在，试确定n及相应的的值;若不存在，请说明理由。
粤公网安备 44130202000953号