把2014个正整数1，2，3，4，…，2015按如图方式排列成一个表.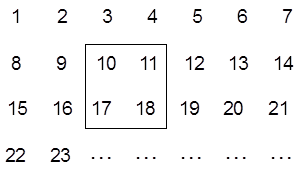
（1）如上图，用一正方形框在表中任意框住4个数，记左上角的一个数为x，则另三个数用含x的式子表示出来，从小到大依次是___________，____________，____________.
（2）当（1）中被框住的4个数之和等于416时，x的值为多少？
（3）在（1）中能否框住这样的4个数，它们的和等于324？若能，则求出x的值；若不能，则说明理由.
相关试题
把2014个正整数1，2，3，4，…，2015按如图方式排列成一个表.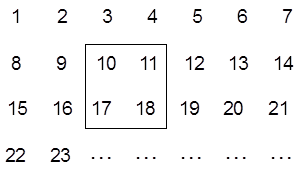
（1）如上图，用一正方形框在表中任意框住4个数，记左上角的一个数为x，则另三个数用含x的式子表示出来，从小到大依次是___________，____________，____________.
（2）当（1）中被框住的4个数之和等于416时，x的值为多少？
（3）在（1）中能否框住这样的4个数，它们的和等于324？若能，则求出x的值；若不能，则说明理由.
中，点
是
的中点，且
⊥
．
的度数；
的长；
为一梯形纸片，
∥
，
．翻折纸片
与点
重合，折痕为
．已知
⊥
.
中，
∥
，
，
⊥
，延长
至点
，使
．
的度数．
为等腰三角形．
中，
是
边上一点，
的延长线交
的延长线于点
，
⊥
，垂足为
，且
．
；
粤公网安备 44130202000953号