如图，半径为1个单位的圆片上有一点Q与数轴上的原点重合（提示:圆的周长C=2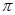
r）
（1） 把圆片沿数轴向左滚动1周，点Q到达数轴上点A的位置，点A表示的数是_________；
（2）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录
如下：+2, -1, -5, +4, +3, -2
①第几次滚动后,Q点距离原点最近？第几次滚动后,Q点距离原点最远？
②当圆片结束运动时，Q点运动的路程共有多少?此时点Q所表示的数是多少?
相关试题
（1）如图所示，∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，求∠MON的度数．
（2）如果（1）中∠AOB=α，其他条件不变，求∠MON的度数．
（3）如果（1）中∠BOC=β（β为锐角），其他条件不变，求∠MON的度数．
（4）从（1）（2）（3）的结果你能看出什么规律？
（5）线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法，请你模仿（1）～（4），设计一道以线段为背景的计算题，并写出其中的规律来？
如图，将一幅角板的直角顶点叠放在一起．
（1）猜想∠AOC与∠BOD的大小关系，并说明理由；
（2）求∠AOD+∠BOC的度数；
（3）若∠BOD：∠AOD=2：11，求∠BOC的度数．
相关知识点
推荐套卷
粤公网安备 44130202000953号