设数列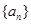 的前
的前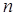 项和为
项和为 ,点
,点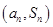 在直线
在直线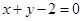 上,
上, .
.
(1)求证:数列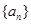 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)设直线 与函数
与函数 的图像交于点
的图像交于点 ,与函数
,与函数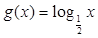 的图像交于点
的图像交于点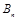 ,记
,记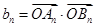 (其中
(其中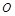 为坐标原点),求数列
为坐标原点),求数列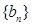 的前
的前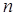 项和
项和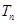 .
.
相关知识点
推荐套卷
设数列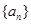 的前
的前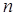 项和为
项和为 ,点
,点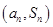 在直线
在直线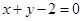 上,
上, .
.
(1)求证:数列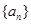 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)设直线 与函数
与函数 的图像交于点
的图像交于点 ,与函数
,与函数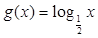 的图像交于点
的图像交于点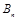 ,记
,记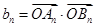 (其中
(其中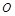 为坐标原点),求数列
为坐标原点),求数列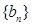 的前
的前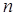 项和
项和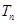 .
.