(本小题满分12分)已知正方形 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点.
(1)在正方形 内部随机取一点
内部随机取一点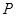 ,求满足
,求满足 的概率;
的概率;
(2)从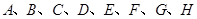 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望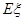 .
.
相关知识点
推荐套卷
(本小题满分12分)已知正方形 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点.
(1)在正方形 内部随机取一点
内部随机取一点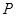 ,求满足
,求满足 的概率;
的概率;
(2)从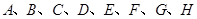 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望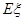 .
.