为迎接“元旦”的到来，某食品连锁店对某种商品进行了跟踪调查，发现每天它的销售价与销售量之间有如下关系：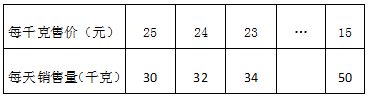
如果单价从最高25元/千克下调到x元/千克时，销售量为y千克，已知y与x之间的函数关系是一次函数：
（1）求y与x之间的函数关系式；
（2）若该种商品成本价是15元/千克，为使“元旦”节这天该商品的销售总利润是200元，那么这一天每千克的销售价应定为多少元？
相关试题
时，由于粗心，误认为加上此式，得到的结果为
，试求此题的正确结果。
－1）2＝0，问单项式3x2ym＋n－1和 x2m－n＋1y4是同类项吗？相关知识点
推荐套卷
为迎接“元旦”的到来，某食品连锁店对某种商品进行了跟踪调查，发现每天它的销售价与销售量之间有如下关系：
如果单价从最高25元/千克下调到x元/千克时，销售量为y千克，已知y与x之间的函数关系是一次函数：
（1）求y与x之间的函数关系式；
（2）若该种商品成本价是15元/千克，为使“元旦”节这天该商品的销售总利润是200元，那么这一天每千克的销售价应定为多少元？
粤公网安备 44130202000953号