有一种可食用的野生菌，刚上市时，外商李经理以每千克30元的市场价格收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这种野生菌在冷库中最多保存140天，同时，平均每天有3千克的野生菌损坏导致不能出售．
（1）若存放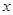
天后，将这批野生菌一次性出售，设这批野生菌的销售总额为
元，试求出与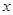之间的函数关系式；
（2）李经理将这批野生菌存放多少天后一次性全部出售可以获得22500元的利润？
相关试题
，
，当
时，函数
（
）的最大值与最小值之差是1，求a的值．
某公司欲招聘一名工作人员，对甲、乙两位应聘者进行面试和笔试，他们的成绩（百分制）如下表所示．
若公司分别赋予面试成绩和笔试成绩6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？
．相关知识点
推荐套卷
粤公网安备 44130202000953号