(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB= ,∠XBC+∠XCB= 。
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.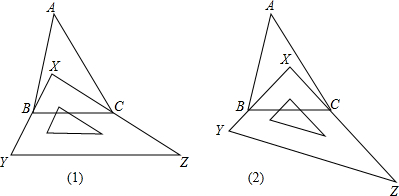
相关知识点
推荐套卷
(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB= ,∠XBC+∠XCB= 。
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.