如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF 
平面ABCD，BF=3，G，H分别是CE和CF的中点、
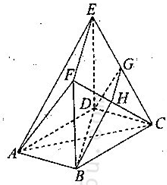
（1）求证：AF//平面BDGH:
（2）求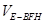
的最大值和最小值
是实数，
，试证明：对于任意
在
上为增函数
SA＝{a＋3}，求a的值．相关知识点
推荐套卷
如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF 平面ABCD，BF=3，G，H分别是CE和CF的中点、
（1）求证：AF//平面BDGH:
（2）求
粤公网安备 44130202000953号