(本题12分)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
相关知识点
推荐套卷

 在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y毫克/升是时间t(小时)的二次函数,已知某病人的三次化验结果如下
在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y毫克/升是时间t(小时)的二次函数,已知某病人的三次化验结果如下 表:
表: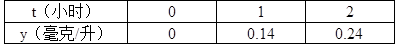

 此大厦大概有多高?请简要
此大厦大概有多高?请简要 说明理由。
说明理由。 粤公网安备 44130202000953号
粤公网安备 44130202000953号