已知△ABC中，∠C=90°，AB=10，AC=6，点O是AB的中点，将一块直角三角板的直角顶点与点O重合并将三角板绕点O旋转，图中的M、N分别为直角三角板的直角边与边AC、BC的交点．
（1）如图①，当点M与点A重合时，求BN的长．
（2）当三角板旋转到如图②所示的位置时，即点M在AC上（不与A、C重合），
①猜想图②中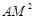
、
、
、
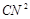之间满足的数量关系式，并说明理由．
②若在三角板旋转的过程中满足CM=CN，请你直接写出此时BN的长．
相关试题
今年以来受各种因素的影响，猪肉的市场价格仍在不断上升。据调查，今年5月份一级猪肉的价格是1月份一级猪肉价格的1. 25倍，小英同学的妈妈同样用20元钱在5月份购得一级猪肉比在1月份购得的一级猪肉少0.4斤，那么今年1月份的一级猪肉每斤是多少元？
你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细（横截面积）xx(mm2)的反比例函数，其图像如上图所示．写出y与x的函数关系式
若当面条的粗细应不小于1.6mm2，面条的总长度最长是多少？
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题画线段AD// BC且使AD =BC连接CD,且四边形ABCD为格点四边形：
△ACD为____ 三角形，四边形ABCD的面积为___
AC与DB相交于点O，△ABO的面积为____．
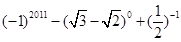
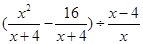
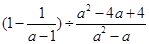
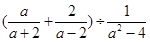，然后选取一个合适的整数a代入求值，其中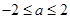
相关知识点
推荐套卷
粤公网安备 44130202000953号