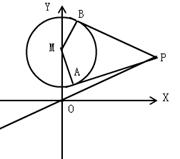
(本小题满分12分)如图, 已知圆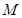 :
: 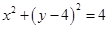 , 直线
, 直线 的方程为
的方程为 , 点
, 点 是直线
是直线 上一动点, 过点
上一动点, 过点 作圆的切线
作圆的切线 、
、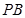 , 切点为
, 切点为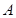 、
、 .
.
(1)当 的横坐标为
的横坐标为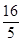 时, 求∠
时, 求∠ 的大小;
的大小;
(2)求证: 经过A、P、M三点的圆 必过定点, 并求出所有定点的坐标.
必过定点, 并求出所有定点的坐标.
相关知识点
推荐套卷
(本小题满分12分)如图, 已知圆 :
: 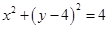 , 直线
, 直线 的方程为
的方程为 , 点
, 点 是直线
是直线 上一动点, 过点
上一动点, 过点 作圆的切线
作圆的切线 、
、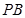 , 切点为
, 切点为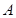 、
、 .
.
(1)当 的横坐标为
的横坐标为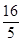 时, 求∠
时, 求∠ 的大小;
的大小;
(2)求证: 经过A、P、M三点的圆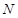 必过定点, 并求出所有定点的坐标.
必过定点, 并求出所有定点的坐标.