（本小题满分12分）标号为0到9的10瓶矿泉水.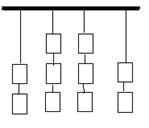
（1）从中取4瓶, 恰有2瓶上的数字相邻的取法有多少种？
（2）把10个空矿泉水瓶挂成如下4列的形式, 作为射击的靶子, 规定每次只能射击每列最下面的一个（射中后这个空瓶会掉到地下）, 把10个矿泉水瓶全部击中有几种不同的射击方案？
（3）把击中后的矿泉水瓶分送给A、B、C三名垃圾回收人员, 每个瓶子1角钱.垃圾回收人员卖掉瓶子后有几种不同的收入结果？
的两顶点为焦点，以椭圆
，一个过点
的双曲线的长轴的端点为椭圆的焦点，求双曲线的标准方程。
，双曲线上一点
到
的距离的差的绝对值等于
，求双曲线的标准方程。
表示焦点在
轴上的双曲线，求
的范围。
的一个焦点为
，求
的值。推荐套卷
（本小题满分12分）标号为0到9的10瓶矿泉水.
（1）从中取4瓶, 恰有2瓶上的数字相邻的取法有多少种？
（2）把10个空矿泉水瓶挂成如下4列的形式, 作为射击的靶子, 规定每次只能射击每列最下面的一个（射中后这个空瓶会掉到地下）, 把10个矿泉水瓶全部击中有几种不同的射击方案？
（3）把击中后的矿泉水瓶分送给A、B、C三名垃圾回收人员, 每个瓶子1角钱.垃圾回收人员卖掉瓶子后有几种不同的收入结果？
粤公网安备 44130202000953号