(本题9分)阅读下列材料,然后解答问题:
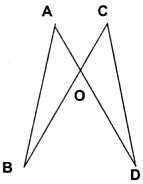
如图(1):AB是⊙O的直径,AD是⊙O切线,BD交⊙O与点C,求证:∠DAC=∠B.
证明:因为AB为直径,AD为切线,所以AB⊥AD,
即∠BAD=900, 故∠DAC+∠BAC=900,
又因为AB是直径,所以∠ACB=900,
即∠BAC+∠B=900,所以∠DAC=∠B.
(1)如图(2):若AB不是⊙O的直径,上述材料中的其他条件不变,那么∠DAC=∠B还成立吗?如果成立,证明你的结论;如果不成立,猜想∠DAC和∠B的大小关系;
(2)若切线AD和弦AC所夹的角∠DAC叫弦切角,那么通过上述的证明,可得出一个结论:弦切角等于它所夹的弧所对的 角.
相关知识点
推荐套卷
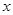 台,A、B两省将捐赠的挖掘机全部调往灾区共耗资
台,A、B两省将捐赠的挖掘机全部调往灾区共耗资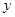 万元。
万元。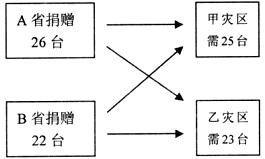
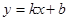 的图象,求
的图象,求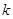 、
、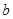 的值,并求
的值,并求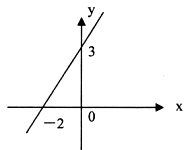
 的算术平方根是3,
的算术平方根是3, 的立方根是2,求
的立方根是2,求 的平方根
的平方根 粤公网安备 44130202000953号
粤公网安备 44130202000953号