拖拉机在行驶的过程中的噪音会影响周围环境，某拖拉机位于A学校正南方向130m的B处，正以120m/min的速度沿公路BC方向行驶，如图所示，已知A学校到BC的距离AD=50m，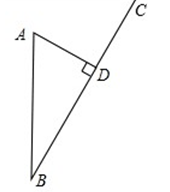
（1）求拖拉机从B处行驶到D处经过多长时间？
（2）如果在距拖拉机100m的圆形区域内都将受噪音影响，那么A学校受到拖拉机噪音影响的时间有多长？（结果精确到0.1，
≈1.732）
相关试题
正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上. 分别连接BD，BF，FD，得到△BFD.
（1）在图中，若正方形CEFG的边长分别为1，3，4，且正方形ABCD的边长均为3，请通过计算填写下表：
正方形CEF G的边长 |
1 |
3 |
4 |
| △BFD的面积 |
（2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S△BFD的大小，并结合图3证明你的猜想.
相关知识点
推荐套卷
粤公网安备 44130202000953号