(本题8分)如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为: (+1,+4),从
(+1,+4),从 (-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
图中 ,
,
若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
若图中另有两个格点M、N,且 ,
,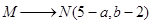 ,则
,则 应记作什么?
应记作什么?
相关知识点
推荐套卷
(本题8分)如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为: (+1,+4),从
(+1,+4),从 (-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
图中 ,
,
若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
若图中另有两个格点M、N,且 ,
,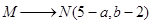 ,则
,则 应记作什么?
应记作什么?