在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.①判断线段MN、BM、CN之间有何数量关系,并证明;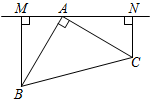
②若AM=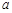 ,BM=
,BM=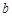 ,AB=
,AB=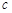 ,试利用图①验证勾股定理
,试利用图①验证勾股定理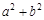 =
=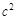 ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)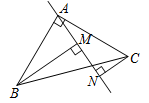
相关知识点
推荐套卷
在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM=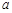 ,BM=
,BM=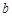 ,AB=
,AB=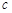 ,试利用图①验证勾股定理
,试利用图①验证勾股定理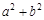 =
=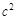 ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)