如图(1),边长为6的等边三角形ABC中,点D沿射线AB方向由A向B运动,点F同时从C出发,以相同的速度沿射线BC方向运动,过点D作DE⊥AC,连结DF交射线AC于点G.
(1)当点D运动到AB的中点时,求AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图(2)的情况时,EG的长始终等于AC的一半吗?若改变,说明理由,若不变,请证明EG等于AC的一半.
相关知识点
推荐套卷
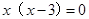
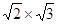
 过点(8,0),
过点(8,0),
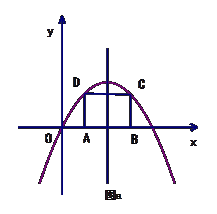
 的值;
的值;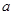 ,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在
,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在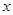 轴上,设矩形ABCD的周长为L,求L的最大值;
轴上,设矩形ABCD的周长为L,求L的最大值; ,抛物线的顶点为E,对称轴与直线
,抛物线的顶点为E,对称轴与直线 交于点F.将直线EF向右平移
交于点F.将直线EF向右平移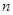 个单位后(
个单位后( 粤公网安备 44130202000953号
粤公网安备 44130202000953号