如图①,在平面直角坐标系中,点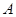 的坐标为
的坐标为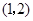 ,点
,点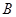 的坐标为
的坐标为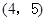 ,二次函数
,二次函数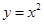 的图象记为抛物线
的图象记为抛物线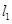 .
.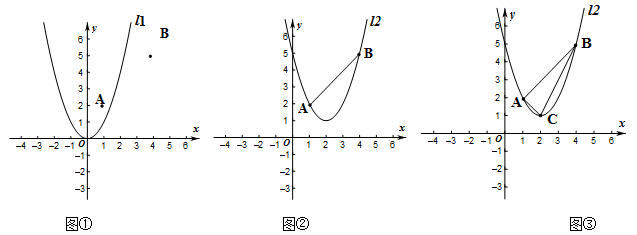
(1)平移抛物线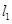 ,使平移后的抛物线过
,使平移后的抛物线过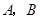 两点,记为抛物线
两点,记为抛物线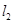 ,如图②,求抛物线
,如图②,求抛物线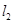 的函数表达式.
的函数表达式.
(2)请在图②上用尺规作图的方式探究抛物线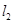 上是否存在点
上是否存在点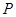 ,使
,使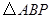 为等腰三角形.若存在,请判断点
为等腰三角形.若存在,请判断点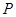 共有几个可能的位置(保留作图痕迹)并在图中画出P点,以P1、P2、P3、、、表示不同的点;若不存在,请说明理由.
共有几个可能的位置(保留作图痕迹)并在图中画出P点,以P1、P2、P3、、、表示不同的点;若不存在,请说明理由.
(3)设抛物线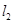 的顶点为
的顶点为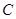 ,
,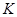 为抛物线
为抛物线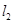 一点.若
一点.若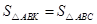 ,求点
,求点 的坐标.
的坐标.
相关知识点
推荐套卷
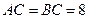 m,
m,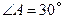 ,
,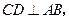 于点
于点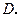

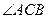 的大小.
的大小.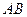 的长度.
的长度. ,其中a=2,
,其中a=2,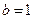 .
. .
. 在第一象限相交于点C;以AC为斜边、
在第一象限相交于点C;以AC为斜边、 为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y=
为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y= 上;直线y=hx+d、双曲线y=
上;直线y=hx+d、双曲线y= 同时经过两个不同的点C,D
同时经过两个不同的点C,D
 粤公网安备 44130202000953号
粤公网安备 44130202000953号