已知：如图，正方形ABCD中，点E是BA延长线上一点，连接DE，点F在DE上且DF=DC，DG⊥CF于G．DH平分∠ADE交CF于点H，连接BH.
（1）若DG=2，求DH的长；
（2）求证：BH+DH=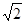
CH.
相关试题
的锐角顶点是直线
与双曲线
在第一象限的交点，且
，
的值
的两个根，求双曲线的函数解析式。
时，它的密度
与V的函数关系式；
时二氧化碳的密度
：
与
平行且过点（3，4），求
，而
与
成反比例，
与
成正比例，并且
时，
；
时，相关知识点
推荐套卷
已知：如图，正方形ABCD中，点E是BA延长线上一点，连接DE，点F在DE上且DF=DC，DG⊥CF于G．DH平分∠ADE交CF于点H，连接BH.
（1）若DG=2，求DH的长；
（2）求证：BH+DH=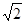CH.
粤公网安备 44130202000953号