(本题6分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.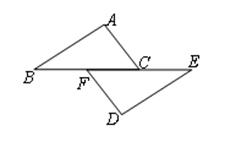
(1)选择的条件是 (填序号)
(2)证明:
相关知识点
推荐套卷
(本题6分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.
(1)选择的条件是 (填序号)
(2)证明: