在一次研究性学习活动中,李平同学看到了工人师傅在木板上画一个直角三角形,方法是(如图):画线段AB,分别以点A,B为圆心,以大于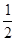 AB的长为半径画弧,两弧相交于点C,连接AC;再以点C为圆心,以AC长为半径画弧,交AC延长线于点D,连接DB.则△ABD就是直角三角形.
AB的长为半径画弧,两弧相交于点C,连接AC;再以点C为圆心,以AC长为半径画弧,交AC延长线于点D,连接DB.则△ABD就是直角三角形.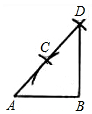
(1)请你说明工人师傅可以这么做直角三角形的理由;
(2)请利用上述方法作一个直角三角形,使其一个锐角为30°(不写作法,保留作图痕迹).
相关知识点
推荐套卷
在一次研究性学习活动中,李平同学看到了工人师傅在木板上画一个直角三角形,方法是(如图):画线段AB,分别以点A,B为圆心,以大于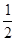 AB的长为半径画弧,两弧相交于点C,连接AC;再以点C为圆心,以AC长为半径画弧,交AC延长线于点D,连接DB.则△ABD就是直角三角形.
AB的长为半径画弧,两弧相交于点C,连接AC;再以点C为圆心,以AC长为半径画弧,交AC延长线于点D,连接DB.则△ABD就是直角三角形.
(1)请你说明工人师傅可以这么做直角三角形的理由;
(2)请利用上述方法作一个直角三角形,使其一个锐角为30°(不写作法,保留作图痕迹).