将两块大小一样含30°角的直角三角板,按如图①与图②方式叠放在一起,使得它们的斜边AB重合,直角边不重合,连结CD.
(1)填空:
图①中CD与AB (填“平行”或“不平行”);
图②中CD与AB (填“垂直”或“不垂直”).并任选一种情况说明理由.
(2)请写出图①中所有的等腰三角形.
(3)若把两块三角板按如图③的方式摆放.已知BC=A1D=4,AC=B1D=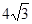 , 试求△AB1C的面积?
, 试求△AB1C的面积?
相关知识点
推荐套卷
将两块大小一样含30°角的直角三角板,按如图①与图②方式叠放在一起,使得它们的斜边AB重合,直角边不重合,连结CD.
(1)填空:
图①中CD与AB (填“平行”或“不平行”);
图②中CD与AB (填“垂直”或“不垂直”).并任选一种情况说明理由.
(2)请写出图①中所有的等腰三角形.
(3)若把两块三角板按如图③的方式摆放.已知BC=A1D=4,AC=B1D=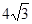 , 试求△AB1C的面积?
, 试求△AB1C的面积?