（本题12分）如图1，在等边△ABC中，点E从顶点A出发，沿AB的方向运动，同时，点D从顶点B出发，沿BC的方向运动，它们的速度相同，当点E到达点B时， D、E两点同时停止运动.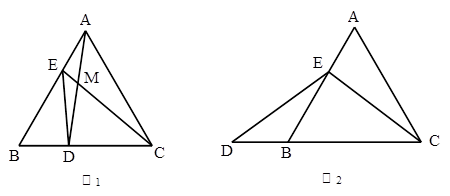
（1）求证：CE＝AD；
（2）连接AD、CE交于点M，则在D、E运动的过程中，∠CMD变化吗？若变化，则说明理由；若不变，则求出它的度数；
（3）如图2，若点D从顶点B出发后，沿BC相反的方向运动，其它条件不变. 求证：CE＝DE.
相关试题
如图，网格中每个小正方形的边长都是1个单位．折线段ABC的位置如图所示．现把折线段ABC向右平移4个单位，画出相应的图形
；把折线段
绕线段
的中点D顺时针旋转90°，画出相应的图形
在上述两次变换中，点
的路径的长度比点
的路径的长度大 个单位．
有4张形状、大小和质地都相同的卡片，正面分别写有字母A，B，C，D和一个算式，背面完全一致．将这4张卡片背面向上洗匀，从中随机抽取1张，不放回，接着再随机抽取1张．请用画树形图或列表法表示出所有的可能结果；（卡片可用A，B，C，D表示）
将“第一张卡片上的算式是正确，同时第二张卡片上的算式是错误”记为事件A，求事件A的概率．
．相关知识点
推荐套卷
粤公网安备 44130202000953号