如图，等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，①猜想 DE与AB的关系？并加以证明。②若Ｐ是ＡＢ延长线一点，Q为BC一点，其他条件不变，结论成吗？画图并证明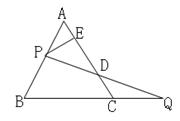
（友情引导：若不知道，你可以动手去量发现结论。若不会，Ｐ是动点，你可以把Ｐ运动到特殊的地方，发现现在可利用什么性质？接下来证明。发现缺少什么？就补什么。若还不会，你能发现有线段相等吗？尝试证明，你会有惊喜。）
相关试题
．
+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．求这条抛物线的解析式；
，且
，求
的值．
条（
）．相关知识点
推荐套卷
粤公网安备 44130202000953号