(本题8分)为提高初中生的身体素质,教育行政部门规定:初中生每天参加户外活动的平均时间应不少于1小时.为了解学生参加户外活动的情况,某县教育行政部门对部分学生参加户外活动的时间进行了抽样调查,并将调查结果绘制成下列两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)这次抽样共调查了 名学生,并补全条形统计图;
(2)计算扇形统计图中表示户外活动时间0.5小时的扇形圆心角度数;
(3)本次调查学生参加户外活动的平均时间是否符合要求?(写出判断过程)

相关知识点
推荐套卷

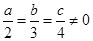 ,且2a-b+c=10.求a、b、c的值.
,且2a-b+c=10.求a、b、c的值.
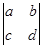 的意义是
的意义是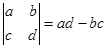 .
.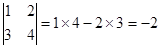 .
.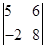 的值.
的值.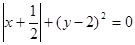 时,
时,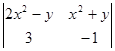 值.
值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号