已知椭圆C1：
+
=1（0＜a＜
，0＜b＜2）与椭圆C2：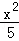
+
=1有相同的焦点．直线L：y=k（x+1）与两个椭圆的四个交点，自上而下顺次记为A、B、C、D．
（Ⅰ）求线段BC的长（用k和a表示）；
（Ⅱ）是否存在这样的直线L，使线段AB、BC、CD的长按此顺序构成一个等差数列．请说明详细的理由．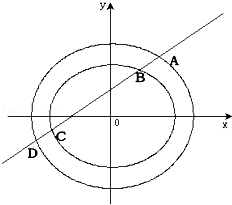
相关试题
2,椭圆
=1，p在椭圆上移动，求
的最小值.
，倾斜角为
的直线L与圆
相交于A、B两点。
，求m的取值范围.
-2z推荐套卷
已知椭圆C1：+=1（0＜a＜，0＜b＜2）与椭圆C2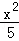：+=1有相同的焦点．直线L：y=k（x+1）与两个椭圆的四个交点，自上而下顺次记为A、B、C、D．
（Ⅰ）求线段BC的长（用k和a表示）；
（Ⅱ）是否存在这样的直线L，使线段AB、BC、CD的长按此顺序构成一个等差数列．请说明详细的理由．
粤公网安备 44130202000953号